ÁREA DE CONHECIMENTO: MATEMÁTICA
COMPETÊNCIA (BNCC)
Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
HABILIDADE (BNCC)
(EF08MA19) – Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.
OBJETIVO
Compreender sobre medidas de área e resolução de problemas utilizando a lógica e linguagens de programação, além de operadores matemáticos.
SEQUÊNCIA DIDÁTICA
Esta sequência didática sugere que sejam elaborados e resolvidos problemas reais envolvendo medidas de área, utilizando recursos tecnológicos como a linguagem de programação Portugol (Português Estruturado), demonstrando a importância e a contribuição da resolução de problemas e lógica na aprendizagem e no desenvolvimento do aluno.

© Freepik
PONTO DE PARTIDA
Para os alunos:
A utilização de recursos tecnológicos, como algoritmos e lógica de programação, é uma alternativa eficiente para solucionar problemas matemáticos.
Com o avanço da tecnologia, a matemática pode ser cada vez mais automatizada, para que não sejam necessários cálculos manuais e repetidos. Assim, problemas cotidianos têm sido cada vez mais fáceis de resolver, pois, quando criamos um algoritmo para solucionar um problema específico, podemos reutilizá-lo, apenas mudando os dados necessários.
A chegada da tecnologia à sala de aula faz com que os alunos tenham que se adaptar, traduzindo o que aprenderam analogicamente para uma outra linguagem, a linguagem de programação, por exemplo.
Nesta atividade, os alunos deverão adaptar os recursos disponíveis do software VisuAlg e sua linguagem de programação Portugol, para trabalharem com problemas de medidas de área, a fim de automatizar o cálculo de valor por metro quadrado de diversas áreas.
O Portugol é uma pseudolinguagem de programação, desprendida das regras formais de linguagens propriamente ditas. Sua construção advém do português (nossa língua materna), sendo mais prático e intuitivo para que pessoas sem o conhecimento prévio de qualquer linguagem, consigam aprender sobre programação.
Para construir um algoritmo em Portugol, devemos conhecer o software em que ele está alocado, o VisuAlg:
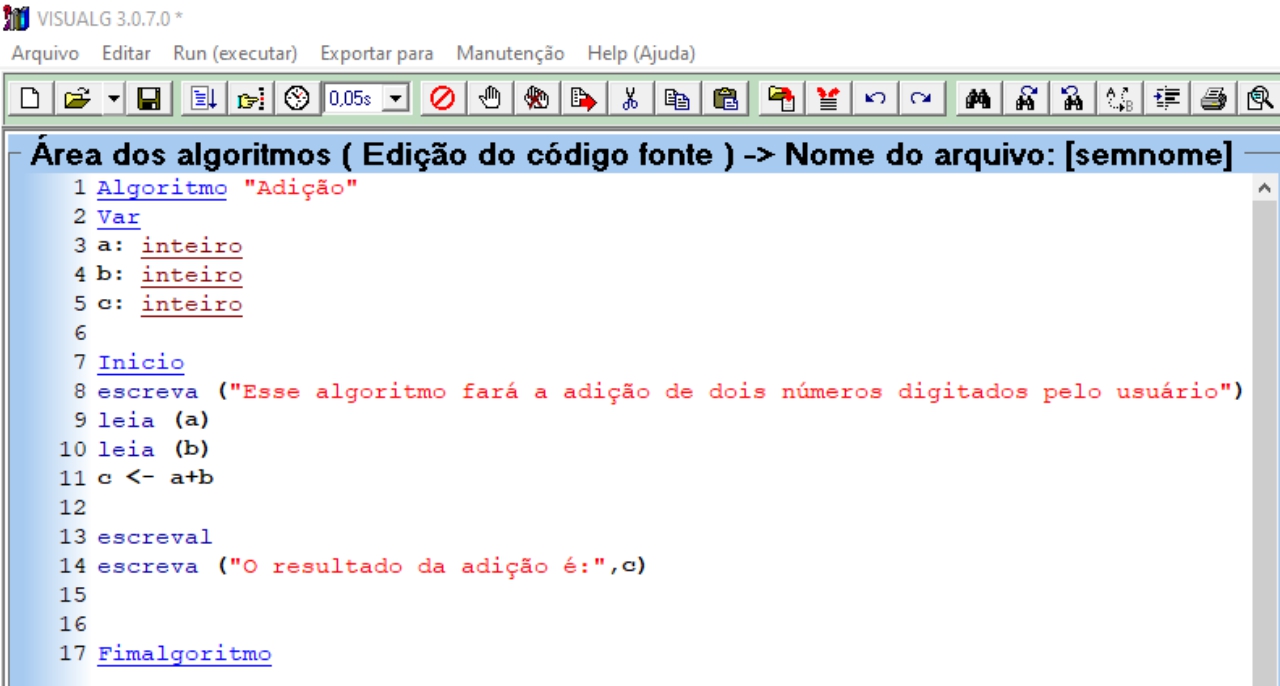
De todas as ferramentas disponíveis no programa, os quatro itens abaixo são os mais importantes. Da esquerda para a direita temos os seguintes botões:
- Novo: cria uma nova página.
- Abrir: abre o gerenciador de tarefas para localizar um algoritmo construído anteriormente.
- Salvar: salva o algoritmo criado.
- Executar: faz com que o computador execute o algoritmo gerado.
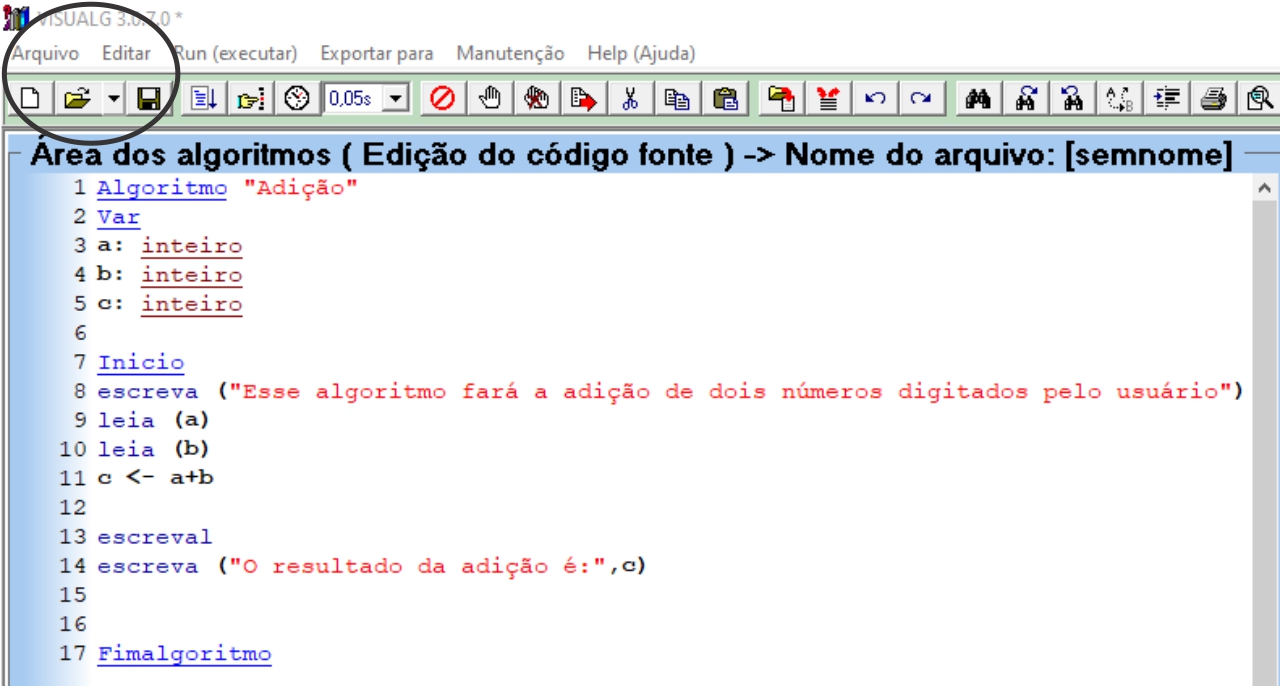
Esta é uma das principais seções quando estamos construindo um algoritmo. A seção chamada de “Var”, é o quadro de variáveis, onde cada variável utilizada dentro do algoritmo é alocada. No print abaixo temos apenas variáveis do tipo “inteiro”, mas existem diversas outras, entre elas:
- Inteiro: variáveis do tipo inteiro, ou seja, números sem casas decimais;
- Real: variáveis do tipo real, ou seja, números que possam, ou não, conter casas decimais;
- Caractere: comporta variáveis do tipo string, ou seja, caracteres (textos e letras);
- Lógico: define variáveis do tipo booleano, consistem em VERDADEIRO, ou FALSO.
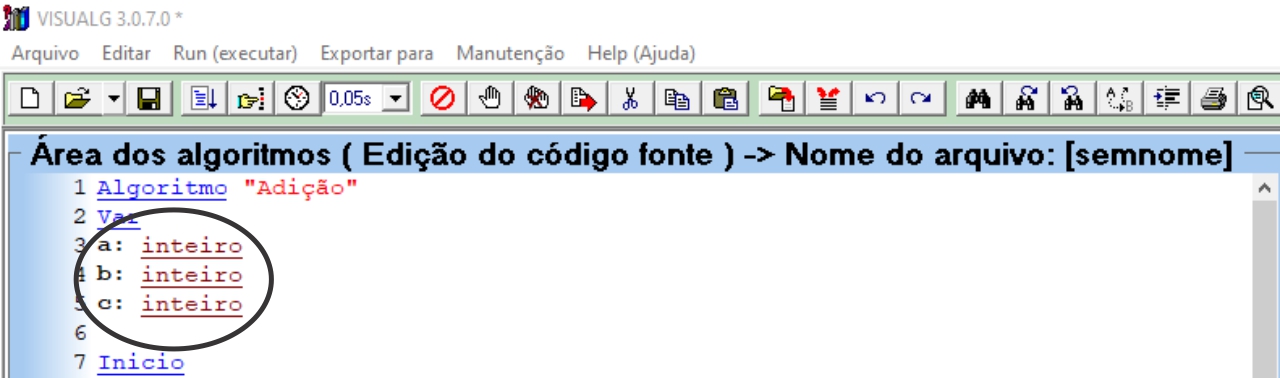
Esta tela é onde toda a criação de algoritmo acontece. Existem comandos básicos para que qualquer algoritmo seja construído, os principais são:
- Comandos de saída de dados:
Escreva: escreve na tela do dispositivo tudo que está dentro da seguinte sentença (<Lista_de_expressão>).
Exemplo de utilização: Escreva (“Olá mundo!”)
Escreval: idêntico ao comando anterior, com a única diferença de pular uma linha.
- Comando de entrada de dados:
Leia: recebe qualquer valor digitado pelo usuário, atribuindo as variáveis que estão listadas no quadro de variáveis, cada uma com sua característica.
Exemplo de utilização: leia (a).
- Comando de atribuição:
<- : Este comando (menor que – <, seguido por um menos) é responsável pela atribuição de valores em uma variável, dependendo de que tipo de variável ela representa. Com o mesmo comando é possível que uma variável assuma o valor de outra.
Exemplo de utilização: VariavelTeste <- 150 + 30.
- Comandos de desvio condicional:
Se: esse é um comando especial, pois ele precisa ser iniciado para funcionar, diferente dos comandos apresentados anteriormente. O “se” é utilizado da seguinte forma:
Se <expressão lógica> entao <expressão lógica>
Códigos do algoritmo…
Fimse
Senao: este comando é utilizado em conjunto com a condicional “se”. Se “tal coisa” acontecer, então. Senão, “tal coisa” acontece.
O “senao” é utilizado da seguinte forma:
Se <expressão lógica> entao <expressão lógica>
Códigos do algoritmo…
Senao <expressão lógica> entao <expressão lógica>
Códigos do algoritmo…
Fimse
- Comandos de repetição:
Para … Faca: esta estrutura serve para repetir parte do algoritmo em um determinado número de vezes.
Exemplo de utilização:
para <variável> de <valor_inicial> ate <valor_limite> [passo <incremento>] faca
códigos do algoritmo
fimpara

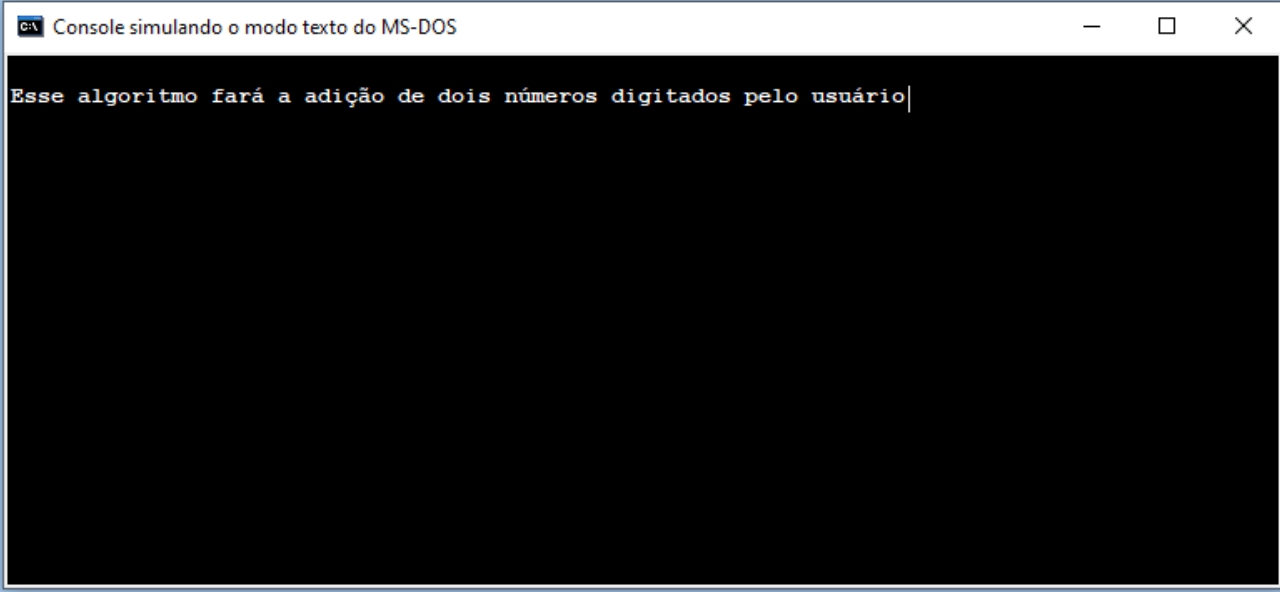
Tela demonstrando um algoritmo sendo executado, com o console apresentando o resultado.
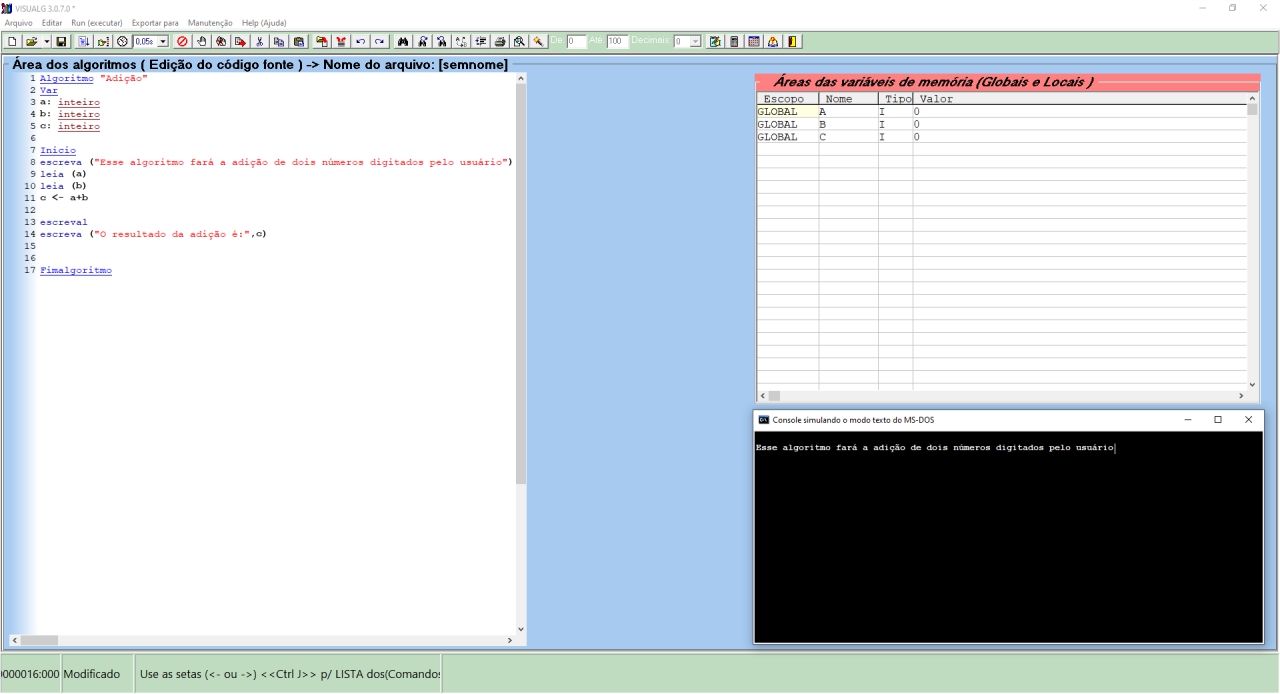
Console de dados: mostra o programa feito pelo algoritmo sendo executado, passo a passo. Dentro desse console, é onde o usuário entra com dados pedidos pelo algoritmo.
PROBLEMATIZAÇÃO
Para os alunos:
Ao trabalharmos com conceitos de medidas, temos que entender que existem diversas unidades quantitativas de medida. No Brasil, usamos o sistema métrico, ou seja, as unidades de medida que usamos são derivadas do metro e cada uma delas está relacionada entre si, sendo as mais comuns: milímetro (mm), centímetro (cm), metro (m) e quilômetro (km). Quando se trata dessas medidas, conseguimos convertê-las umas para outras, segundo a seguinte relação:
Quilômetro (km) -> hectômetro (hm) -> decâmetro (dam) -> metro (m) -> decímetro (dm) -> centímetro (cm)-> milímetro (mm).
Para transformar uma medida em outra, à sua direita, multiplicamos por 10. Se a transformação da unidade não estiver em sequência, a cada “pulo” de casa, é necessário multiplicar por 10 novamente. Acontece a mesma coisa, quando fazemos a transformação para o outro lado, mas dividindo por 10.
Utilizando essa ideia, use a tabela abaixo e transforme 1 quilômetro para hectômetro, até o milímetro. Após isso, faça o contrário, de milímetro para quilômetro. Anote o resultado em uma folha de papel.

ORIENTAÇÕES PARA O PROFESSOR:
Determine o tempo para os alunos realizarem a atividade (cerca de quinze minutos são suficientes).
Se os alunos não conseguirem resolver a questão dentro do tempo determinado, sugira que terminem em casa e de forma individual. Se achar melhor, peça para que dois alunos resolvam a questão no quadro (que cada um faça uma parte) e, se necessário, ajude-os.
Solução:
1) 1km x 10 = 10hm
10hm x 10 = 100dam
100dam x 10 = 1000m
1000m x 10 = 10000dm
10000dm x 10 = 100000cm
100000cm x 10 = 100000mm
2) 1mm : 10 = 0,1cm
0,1cm : 10 = 0,01dm
0,01dm : 10 = 0,001m
0,001m : 10 = 0,0001dam
0,0001dam : 10 = 0,00001hm
0,00001hm : 10 = 0,000001km
INTERVENÇÃO
Para os alunos:
Quando se trata da área de uma superfície, o cálculo acontece por meio do produto do comprimento e largura, por exemplo:
1m x 1m = 1m²
Portanto, a conversão de uma unidade de medida para outra, acontece de uma forma diferente. De 1m² para 1dm², é necessário multiplicar por 100, por exemplo:
Para converter 4m² para dm², fazemos:
4m² x 100 = 400dm²
Consequentemente, de dm² para m², você precisa dividir por 100.
Qual dificuldade você encontrou? Compreendeu como funciona a unidade de medida brasileira? Converse com seu professor (ou professora) e colegas a respeito.
Vamos colocar em prática? Crie um programa utilizando tudo o que você aprendeu até o momento para resolver o seguinte problema:
João comprou um terreno de 30m de largura e 50m de comprimento. Ele quer separar o terreno em três partes iguais. Cada uma dessas partes deverá ter, respectivamente, um terço, metade e um quarto de área construída. Qual é a metragem que poderá ser construída em cada um dos terrenos?
ORIENTAÇÕES PARA O PROFESSOR:
Oriente os alunos sobre a identificação de quando utilizar as unidades de medidas padrões e quando usá-las na sua forma quadrada. Mostre a eles a importância de saber diferenciar esses dois tipos de unidade.
Algumas dúvidas surgirão, principalmente na utilização da metragem quadrada, promova uma discussão entre os estudantes para saná-las.
Se possível, mostre como fazer a conversão de unidades de medida no quadro.
Você poderá abordar temas presentes no cotidiano deles e que fazem parte desse “mundo métrico”, como velocidade, por exemplo.
Deixe a imaginação dos alunos livre para a construção do programa, desde que obtenham o resultado esperado. Cada algoritmo é único, portanto, não existe apenas uma solução.
Solução:
Algoritmo “construção terreno”
Var
tamanho: inteiro
terreno1: real
terreno2: real
terreno3: real
area: real
Inicio
tamanho <- 30*50
terreno1 <- tamanho/3
terreno2 <- tamanho/3
terreno3 <- tamanho/3
terreno1 <- terreno1/3
terreno2 <- terreno1/2
terreno3 <- terreno1/4
area <- terreno1+terreno2+terreno3
escreva (“a área de todo o terreno, é de: “, tamanho,”m²”)
escreva (“a área que irá ser construída é de: “, área,”m²”)
Fimalgoritmo
CRIAÇÃO/AVALIAÇÃO
Para os alunos:
- Crie um programa que seja capaz de ler as medidas de um terreno.
- Adicione a possibilidade de o usuário informar o valor do metro quadrado do local onde o terreno está.
- Faça com que o programa mostre na tela para o usuário o valor total do terreno.
ORIENTAÇÕES PARA O PROFESSOR:
Solução:
Algoritmo “valor metro quadrado”
Var
L: real
C: real
medida: real
preco: real
resultado: real
Inicio
escreva (“digite, em metros, a largura e o comprimento do terreno: “)
leia (L)
leia (C)
medida <- L*C
escreva (“qual o preco do metro quadrado? “)
leia (preco)
resultado <- preco*medida
escreva (“o terreno mede “, medida, “m2 e o preco dele, é de: “, resultado, ” reais”)
Fimalgoritmo
COMPARTILHAMENTO
Para os alunos:
Todo trabalho desenvolvido, seja individual ou em equipe, deve ser compartilhado em um espaço adequado. Faça uma mostra em sala de aula e, posteriormente, com toda a comunidade escolar (docentes, discentes, colaboradores, pais ou responsáveis) para que o trabalho não se torne apenas mais um. Busque formas de divulgação em sua unidade de ensino, seja por meio de mídias sociais ou mostrando aos colegas de outras turmas.

