ÁREA DE CONHECIMENTO: Matemática
COMPETÊNCIA (BNCC)
Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
HABILIDADE (BNCC)
(EF07MA26) – Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um triângulo qualquer, conhecidas as medidas dos três lados.
OBJETIVO
Compreender a construção matemática de triângulos, utilizando recursos tecnológicos, como algoritmos e fluxogramas.
SEQUÊNCIA DIDÁTICA
Esta sequência didática apresenta o conceito de fluxograma, as suas principais simbologias, a compreensão e a criação de um algoritmo e um fluxograma da construção de um triângulo, além de revelar porque não se pode criar um triângulo com segmentos de retas quaisquer.
© Tasha Vector/Shutterstock
PONTO DE PARTIDA
Para os alunos:
A matemática é uma ciência exata que busca encontrar soluções de problemas cotidianos, utilizando fatos, dados e a lógica. Ela foi sendo construída durante toda a história, e hoje, com todos os recursos tecnológicos que temos, conseguimos extrair tudo, além de facilitar o que há de melhor nessa ciência.
A matemática pode ser subdividida da seguinte maneira:
- Aritmética: parte da matemática que trabalha com as operações matemáticas (soma, subtração, multiplicação e divisão).
- Álgebra: é o ramo que estuda a manipulação de fórmulas, polinômios, estruturas algébricas, além da aplicação das operações matemáticas.
- Geometria: estuda todas as formas geométricas (área, volume e comprimento) e a resolução de problemas envolvendo essas figuras.
Nesta atividade, os alunos farão um fluxograma para criar um algoritmo para a construção de um triângulo, utilizando a regra de existência de um triângulo e o software draw.io (software de criação de fluxograma).
PROBLEMATIZAÇÃO
Para os alunos:
A trigonometria é a parte da matemática que estuda a relações entre lados e ângulos entre triângulos.
Para que um triângulo possa existir, ele deve cumprir a sua regra de existência. Pesquise e anote em uma folha de papel que regra é essa.
A seguir, verifique se as medidas abaixo podem se tornar um triângulo. Se não for possível essa construção, diga o motivo.
- 5 cm, 9 cm, 10 cm
- 3 cm, 6 cm, 9 cm
- 5 cm, 10 cm, 15 cm
- 7 cm, 49 cm, 22 cm
- 1 cm, 2 cm, 3 cm
ORIENTAÇÕES PARA O PROFESSOR:
Estipule o tempo máximo para que os alunos realizem a atividade (cerca de quinze minutos são suficientes). Proponha que a resolução seja individual.
Caso algum aluno não consiga terminar toda a tarefa, é possível concluí-la em casa.
Solução:
1. |10 – 9| < 5 < |10 + 9| = |-1| < 5 < |19| = 1 < 5 < 19
|9 – 5| < 5 < |9 + 5| = |4| < 5 < |14| = 4 < 5 < 14
|5 – 10| < 5 < |5 + 10| = |-5| < 5 < |15| = 5 < 5 < 15
Portanto, pode ser triângulo.
2. |3 – 6 | < 9 < |3 + 6| = |-3| < 9 < |9| = 3 < 9 < 9
|6 – 9| < 3 < |6 + 9| = |-3| < 3 < |15| = 3 < 3 < 15
|9 – 3| < 6 < |9 + 3| = |6| < 6 < |12| = 6 < 6 < 12
Portanto, pode ser triângulo.
3. |5 – 10| < 15 < |5 + 10| = |-5| < 15 < |15| = 5 < 15 < 15
|10 – 15| < 5 < |10 + 15| = |-5| < 5 < |25| = 5 < 5 < 25
|15 – 5| < 10 < |15 + 5| = |10| < 10 < |20| = 10 < 10 < 20
Portanto, pode ser triângulo.
4. |7 – 49| < 22 < |7 + 49| = |-42| < 22 < |56| = 42 > 22 < 52
|49 – 22| < 7 < |49 + 22| = |27| < 7 < |71| = 27 > 7 < 71
|22 – 7| < 49 < |22 + 7| = |15| < 49 < |29| = 15 > 49 > 29
Portanto, NÃO pode ser triângulo.
5. |1 – 2| < 3 < |1 + 2| = |-1| < 3 < |3| = 1 < 3 < 3
|2 – 3| < 1 < |2 + 3| = |-1| < 1 < |5| = 1 < 1 < 5
|3 – 1| < 2 < |3 + 1| = |2| < 2 < |4| = 2 < 2 < 4
Portanto, pode ser triângulo.
INTERVENÇÃO
Para os alunos:
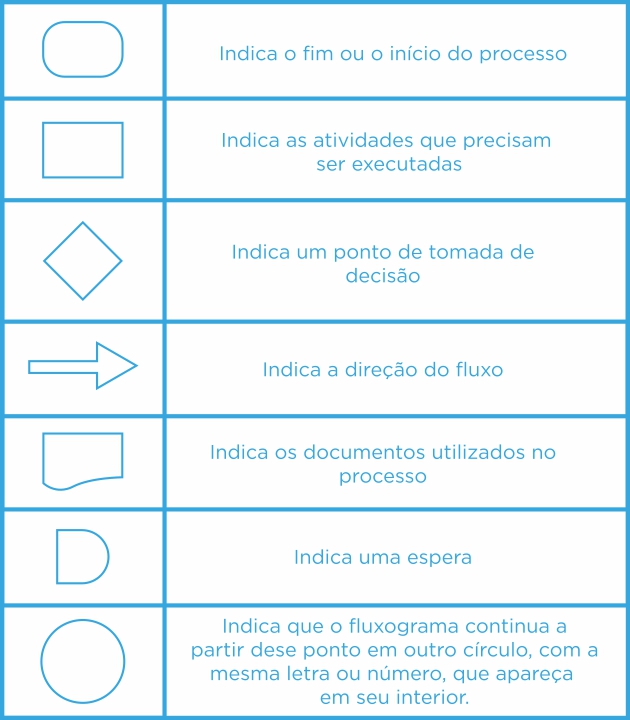
Fluxograma é um diagrama com a finalidade de representar todos os passos de um processo, deixando-os mais claros. Ele tem sempre início, meio e fim, e é composto de símbolos básicos.
As principais simbologias são as seguintes:
Abra o software Draw.io e crie um fluxograma de um algoritmo que faça o cálculo do Teorema de Pitágoras, onde o usuário entre com os dados que precisam ser calculados.
Encontrou alguma dificuldade? Converse com seu professor (ou professora) e colegas sobre as funções e dificuldades de produzir um fluxograma e como ele pode ajudar na criação de um software, por exemplo.
ORIENTAÇÕES PARA O PROFESSOR:
Oriente os alunos sobre cada símbolo do fluxograma e apresente um exemplo para cada um deles.
Promova uma discussão sobre a importância da criação de um fluxograma antes de realizar a construção de um algoritmo, por exemplo. Mencione também o quanto um fluxograma pode ser relevante em uma empresa.
Deixe os alunos livres durante a produção do fluxograma, e que investiguem cada símbolo, descobrindo o que cada um faz e quais resultados podem obter por meio desse método de criação e organização de algoritmos.
CRIAÇÃO/AVALIAÇÃO
Para os alunos:
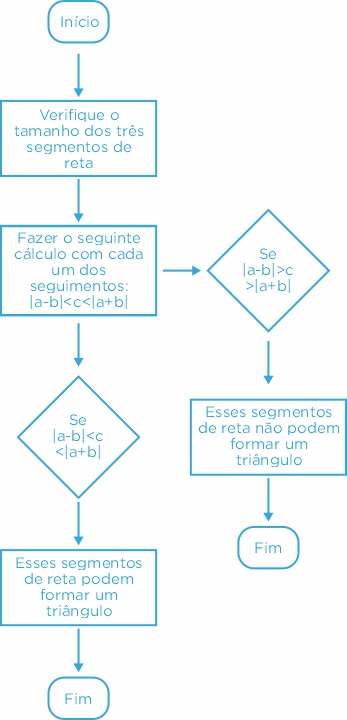
- Crie um fluxograma onde um algoritmo seja construído.
- Esse algoritmo deve conter as informações sobre a regra de existência de um triângulo.
ORIENTAÇÕES PARA O PROFESSOR:
Solução:
COMPARTILHAMENTO
Para os alunos:
Todo trabalho desenvolvido, seja individual ou em equipe, deve ser compartilhado em um espaço adequado. Faça uma mostra em sala de aula e, posteriormente, com toda a comunidade escolar (docentes, discentes, colaboradores, pais ou responsáveis) para que o trabalho não se torne apenas mais um. Busque formas de divulgação em sua unidade de ensino, seja por meio de mídias sociais ou mostrando aos colegas de outras turmas.

