ÁREA DE CONHECIMENTO: MATEMÁTICA
COMPETÊNCIA (BNCC):
- Geral:
Competência 1 – Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
- Específicas:
Competência 2 – Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo;
Competência 3 – Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
HABILIDADE (BNCC):
(EF03MA03) – Construir e utilizar fatos básicos da adição e da multiplicação para o cálculo mental ou escrito;
(EF03MA05) – Utilizar diferentes procedimentos de cálculo mental e escrito, inclusive os convencionais, para resolver problemas significativos envolvendo adição e subtração com números naturais;
(EF03MA06) – Resolver e elaborar problemas de adição e subtração com os significados de juntar, acrescentar, separar, retirar, comparar e completar quantidades, utilizando diferentes estratégias de cálculo exato ou aproximado, incluindo cálculo mental.
OBJETIVO
Propor diferentes procedimentos de cálculo mental, comparando com o conceito de Decomposição, em que os problemas são divididos em partes menores.
SEQUÊNCIA DIDÁTICA
No documento da BNCC (2018), o trabalho com cálculo mental é apontado na unidade temática Números, em uma perspectiva de que o trabalho seja realizado por meio de diferentes estratégias para obtenção de resultados em relação aos cálculos. É enfatizado ainda que esse trabalho deve se dar por proposições de problemas em que os estudantes se sintam desafiados a argumentar e justificar os procedimentos utilizados para a resolução.
Assim, ao propor situações de análise de estratégias pensadas de forma individual pelos estudantes, comparando-as com os métodos elaborados pelos colegas, encorajando-os a desenvolver, registrar, explicar, entender, refutar e sugerir, o estudante passa a ter embasamento e condições de conhecer e estabelecer quais técnicas podem ser mais adequadas para realizar cálculos mentais.
A questão do registro e da análise é um importante passo para estabelecer as bases que possibilitam o desenvolvimento do cálculo mental. Trabalhar essas estratégias de maneira conjunta ao eixo do Pensamento Computacional e o conceito de Decomposição é uma forma de comparar e demonstrar aos estudantes que analisar os problemas, dividindo-os em partes menores, pode ser um processo que torna mais fácil a sua resolução.
Ao trabalhar com o conceito de Decomposição, referente ao Pensamento Computacional, ainda temos a questão da possibilidade de aumentar a atenção às partes do problema, aos detalhes. O nível de atenção é um dos requisitos para o funcionamento da memória. Um dos mecanismos para o cálculo mental é a memorização. Seja com a memorização de métodos ou até mesmo a memorização de resultados, em cálculos mais simples, a função cognitiva da memória é uma das que mais utilizamos em nosso dia a dia, assim, técnicas de cálculo mental podem ser muito úteis.
A proposta apresentada trabalha com uma sequência de atividades para debater sobre a ideia tão difundida da “conta de cabeça”.

© NadyaEugene/Shutterstock
PONTO DE PARTIDA
ORIENTAÇÕES PARA O PROFESSOR:
Comente sobre as peças do computador que dão a ele a capacidade de “lembrar como executar um comando”. Duas peças trabalham em conjunto para serem a “memória” do computador.
Uma é a memória RAM, que é um espaço temporário de armazenamento de dados. Esses dados são acessados e apresentados de forma super rápida.
A outra é o HD, também chamado de disco rígido, que armazena dados de maneira efetiva, ou seja, independentemente se o computador estiver ligado ou desligado, as informações salvas permanecem guardadas.
Explique que essa situação representa um pouco a memória do ser humano, pois nós temos uma memória de curto prazo, por exemplo, conseguimos memorizar um número de telefone que alguém acabou de falar, mas provavelmente se não registrarmos esse número, em breve acabaremos o esquecendo. E temos a memória de longo prazo, que são as coisas que lembramos por mais tempo. Como nós seres humanos temos a capacidade da emoção, uma memória pode ser algo tão forte que fica conosco por tempo indefinido, e mesmo que tenhamos algum problema relacionado ao nosso cérebro, “o nosso HD”, se a memória for muito importante, temos a capacidade de não esquecê-la.
Mas por qual razão falar disso? Comente com os alunos que quando falamos em cálculos na matemática, é natural que a gente use a nossa memória e muitas pessoas dizem que fazem contas de cabeça. Pergunte a eles o que isso quer dizer. Mencione sobre a capacidade que algumas pessoas têm de responder perguntas sobre cálculos de forma muito rápida, e questione o que eles imaginam que é necessário para adquirir essa habilidade.
Para os alunos:
A discussão sobre a memória do computador e memória do ser humano pode ser aprofundada com o texto: “O que é memória RAM e qual a sua importância?” disponível em http://bit.ly/RAMartigo. O trecho do texto a seguir traz a comparação entre as duas peças:
“Vamos imaginar que a memória RAM seja a sua escrivaninha. Seu espaço de trabalho, onde você faz anotações rápidas, é o topo da mesa. Você precisa ter tudo à mão para encontrar rapidamente as coisas que precisa. Isso é a memória RAM. Em contraste, se você quer guardar algo para trabalhar em outro momento, você coloca aquilo na gaveta da escrivaninha – ou armazena no HD…”
Então, para criar uma estratégia de execução de um cálculo mental, precisamos ter um espaço de trabalho em nosso cérebro, “uma escrivaninha”, para ter as ferramentas à mão, no caso, acessamos em nosso cérebro o que já aprendemos sobre números. Quando assimilamos um método de calcular, guardamos essa informação em outro espaço da nossa memória.
Vamos resolver o problema a seguir usando apenas o cálculo mental, depois, compartilharemos com os amigos a forma que cada um pensou:
Os irmãos Lara e Pedro foram a uma lanchonete. Lara pediu uma pizza e um sorvete, que custaram 13 reais. Pedro pediu um sanduíche e um refrigerante, que custaram 18 reais. Eles juntaram o dinheiro que tinham guardado e levaram 40 reais. Isso foi suficiente para o pagamento? Sobrou alguma coisa?
PROBLEMATIZAÇÃO
ORIENTAÇÕES PARA O PROFESSOR:
Peça que os estudantes conversem sobre o problema e a forma como calcularam. Pergunte se teriam feito diferente se estivessem utilizando um papel. Comente que, em alguns momentos temos em mãos um instrumento que nos ajuda a calcular como, calculadoras, folhas para registro e confirmação do cálculo, mas que em outras situações, quando envolve a utilização de dinheiro, precisamos de respostas rápidas e o que nos dá a segurança para saber se o cálculo mental está correto é a estratégia utilizada. Por isso, é importante pensar, registrar e analisar as estratégias.
Lance a pergunta: Fazemos cálculos de cabeça ou com a cabeça?
Detalhando a problemática para os alunos comente: começamos conversando sobre como a memória pode auxiliar no cálculo mental, depois fizemos uma experiência resolvendo um problema e discutindo sobre as estratégias. A função de calcular é muito associada ao computador, aliás, a palavra computador, antes de termos a utilização das máquinas, se referia a pessoa que computava, ou seja, que calculava.
Para os alunos:
Há uma grande diferença entre a pessoa que calcula e o computador, o computador é programado, ou seja, segue instruções e é capaz de fazer isso de maneira mais rápida que uma pessoa, no entanto, é dependente da programação. Uma palavra que ouviremos muito é “algoritmo”, seu significado é: um processo que envolve uma sequência finita de passos que levam à solução de um problema. O programador prepara um algoritmo, dividindo os passos que o computador deve executar, esse processo é conhecido como “Decomposição” de um problema. Os problemas são divididos em passos menores e mais fáceis de resolver, há rigorosidade aos detalhes, seguindo uma instrução de acordo com o que foi planejado e é assim que o computador calcula. Fazendo uma brincadeira, podemos dizer que o computador tem a capacidade de fazer um cálculo de maneira tão rápida, porque ele consegue “fazer a conta de cabeça”.
Da mesma forma que o computador vai executando os processos passo a passo, nós também podemos usar a Decomposição pensando em uma boa estratégia para resolver um cálculo. No entanto, nós somos capazes de construir um método e, aos poucos, modificá-lo e aperfeiçoá-lo para solucionar um cálculo, sem depender de um programador.
Nesse caso, é possível afirmar que as pessoas fazem cálculos “com a cabeça”, pois, primeiramente o problema é analisado, planeja-se uma forma de resolução e coloca-se em prática o que foi pensado.
E quanto de memória sobre estratégias para a resolução de cálculos precisamos ter? Em um computador, quanto mais capacidade de memória RAM ele tem, mais rápido ele executa as suas tarefas. Para aumentar a nossa memória sobre estratégias de cálculo, vamos conhecer métodos diferenciados.
INTERVENÇÃO
ORIENTAÇÕES PARA O PROFESSOR:
Comente que a memória rápida para calcular, se refere a um cálculo que já fizemos tantas vezes que a resposta se torna automática. Por exemplo, é provável que você já tenha arrumado os pratos na mesa para a refeição da sua família diversas vezes e, automaticamente, sabe quantos pratos são necessários. Mas se você fizer isso quando estiver recebendo visitantes na sua casa, precisará contar quantas pessoas participarão da refeição antes de pegar os pratos, e essa conta não é automática.
Então, é natural que alguns cálculos envolvendo números menores fiquem registrados em nossa memória. Na matemática essa agilidade de pensamento, essa memória rápida é nomeada como “fato básico” e se refere aos cálculos, geralmente com números de um só algarismo que são realizados mentalmente, por exemplo: 3 + 4 =7 6 + 6 = 12 9 + 5 = 14.
Quando acessamos em nossa memória que contém fatos básicos, lembramos dessas contas, um bom exemplo disso é a tabuada, e isso nos ajuda a calcular mentalmente quando a situação-problema envolve números maiores.
Peça aos alunos para indicarem todos os fatos básicos (adições) possíveis resultantes em 5:
0 + 5 = 5
1 + 4 = 5
2 + 3 = 5
3 + 2 = 5
4 + 1 = 5
5 + 0 = 5
Uma situação um pouco mais desafiadora pode ser proposta por meio do jogo “Somando 10”, disponível em https://www.ensinandomatematica.com/falando-sobre-adicao/.
Objetivo: obter a soma 10 adicionando quatro números (cartas) enfileirados na vertical, horizontal ou diagonal;
Material necessário: tabuleiro quadriculado de 32 cm x 32 cm (modelo), cartinhas de 7 cm x 7 cm distribuídas da seguinte forma: numeral 1 (20 cartinhas), numeral 2 (20 cartinhas), numeral 3 (15 cartinhas), numeral 4 (10 cartinhas), numeral 5 (5 cartinhas), numeral 6 (2 cartinhas);

Participantes: grupos de 3 ou 4 estudantes;
Modo de jogar: Inicialmente, as cartinhas são embaralhadas e cada jogador retira 3 cartas para iniciar as jogadas. As demais ficam viradas para baixo em uma pilha. Cada jogador, na sua vez, deve colocar uma carta em um quadradinho do tabuleiro. O competidor que conseguir colocar a quarta carta que feche a soma 10 em uma linha, coluna ou diagonal, toma as quatro cartas para si e marca um ponto. As cartas tomadas do tabuleiro não retornam ao jogo (são colocadas de lado). O jogador deve retirar uma carta do monte sempre que retirar uma de seu trio de cartas.
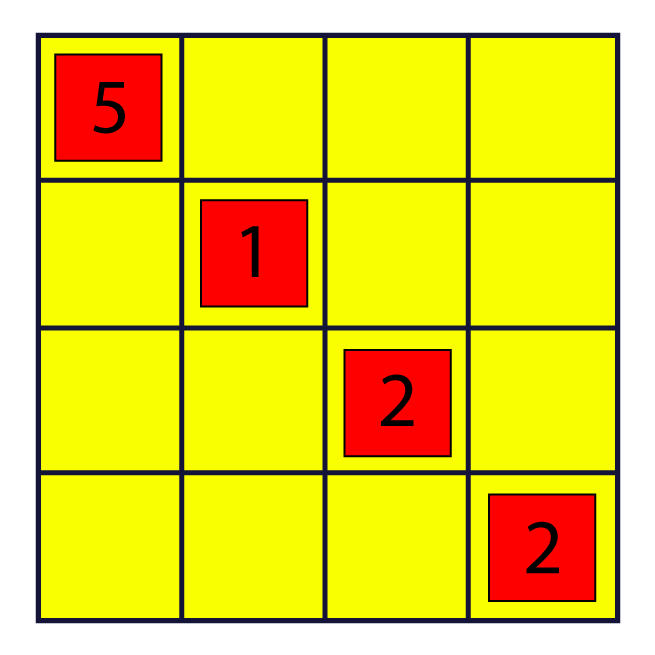
Qualquer carta pode ser colocada em qualquer quadradinho do tabuleiro, mesmo que a soma da linha, coluna ou diagonal em que ela esteja seja diferente de 10. Porém o ponto é marcado pelo jogador que conseguir fechar a soma 10 a partir da colocação de sua cartinha em uma fileira que já possui outras três cartas.
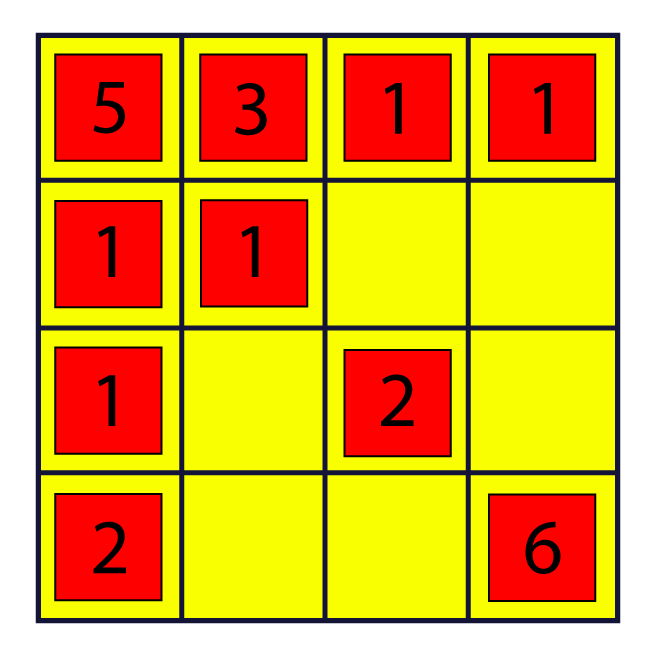
No caso de não haver mais cartinhas para retirar do monte, passa-se a vez. O jogo termina quando um dos competidores não dispuser de números para colocar no tabuleiro ou quando este estiver completo e nenhum quarteto de cartinhas possa ser retirado. É vencedor aquele que fizer mais pontos.
Depois de jogarem, peça que os grupos apresentem para a turma alguma situação que ocorreu nas jogadas. Por exemplo: 5+2+2+1=10 ou 3+3+3+1=10, e discutam sobre os resultados.
Comente que, em se tratando de cálculos com números maiores, algumas estratégias podem ser utilizadas.
Vamos começar pela estratégia de decomposição. Questione se eles já têm uma pista sobre como desenvolver a estratégia, apresente um cálculo e explique a forma de resolução.
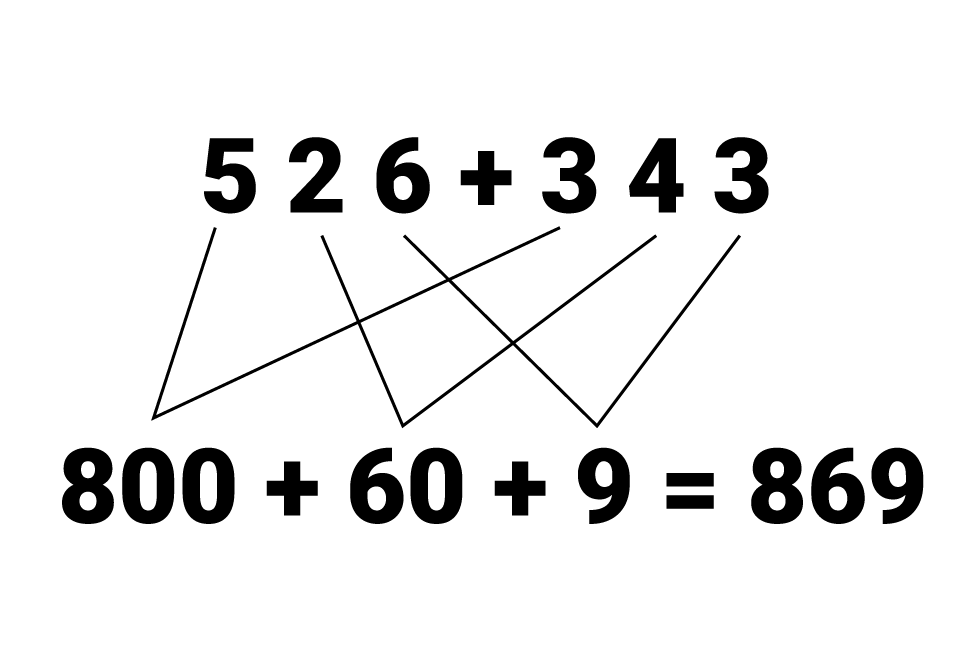
A estratégia de compensação é utilizada para arredondar os números e facilitar o cálculo mental:
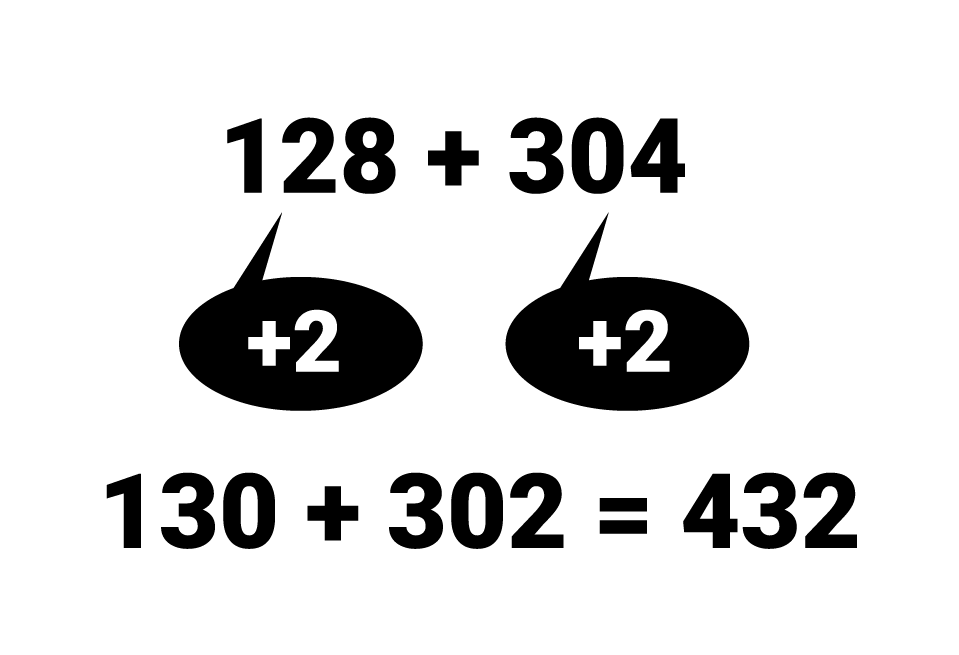

Na estratégia comutativa, é possível primeiro juntar os números em que a soma possa ser mais fácil e dessa soma juntar o número restante:
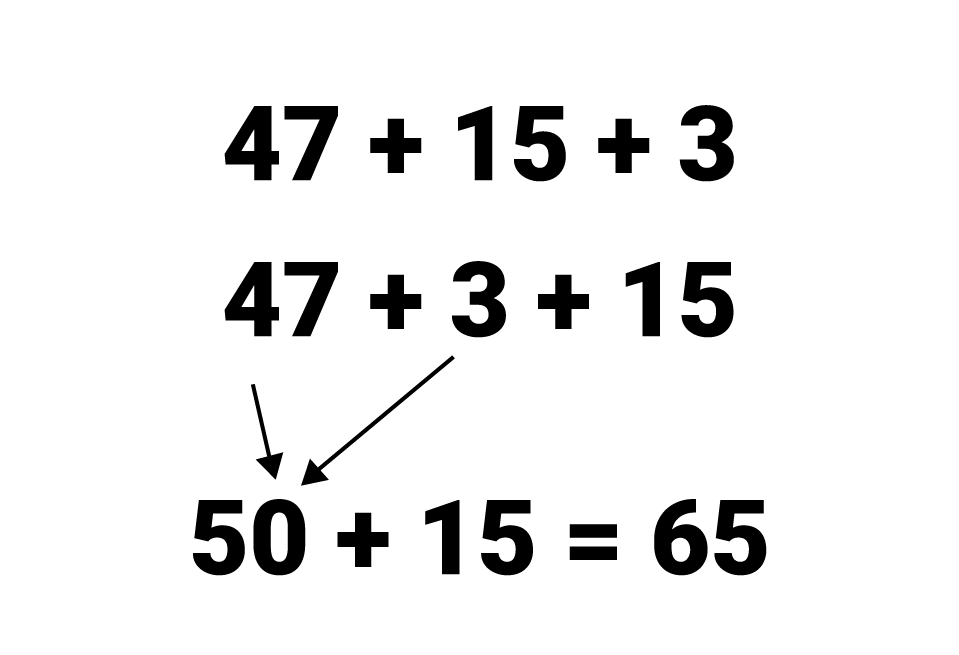
A estratégia da decomposição também pode ser utilizada na subtração:
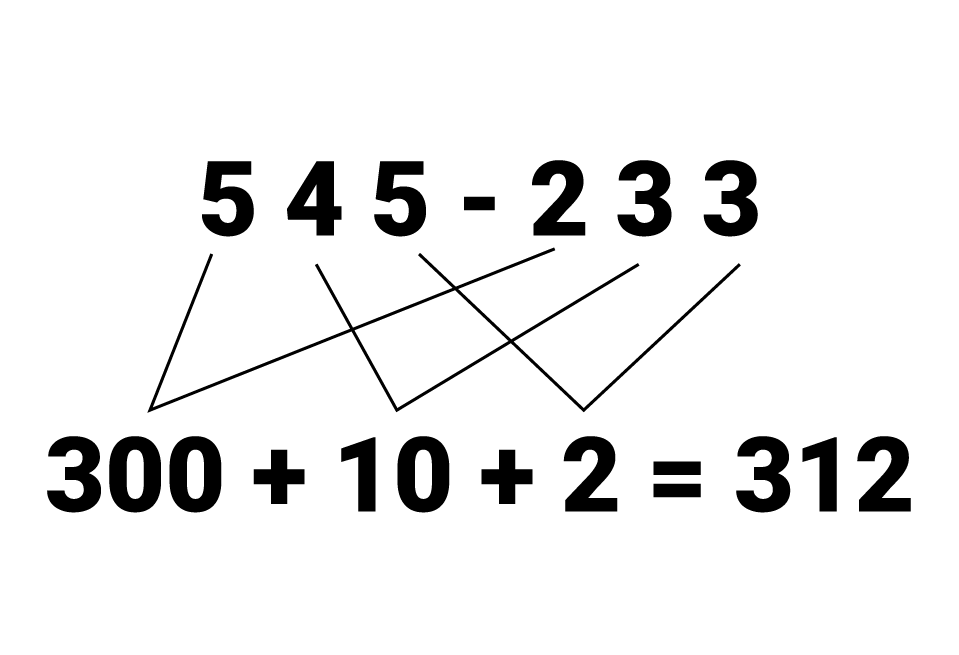
Existe a possibilidade de realizar um cálculo dividindo-o em partes de uma maneira diferente:
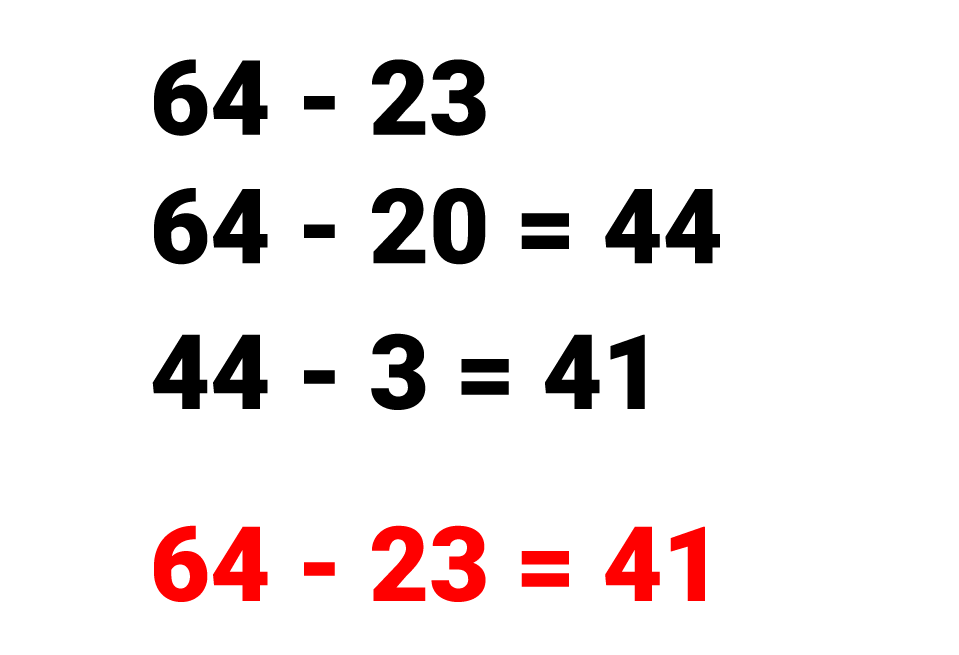
Isso também é possível na multiplicação:
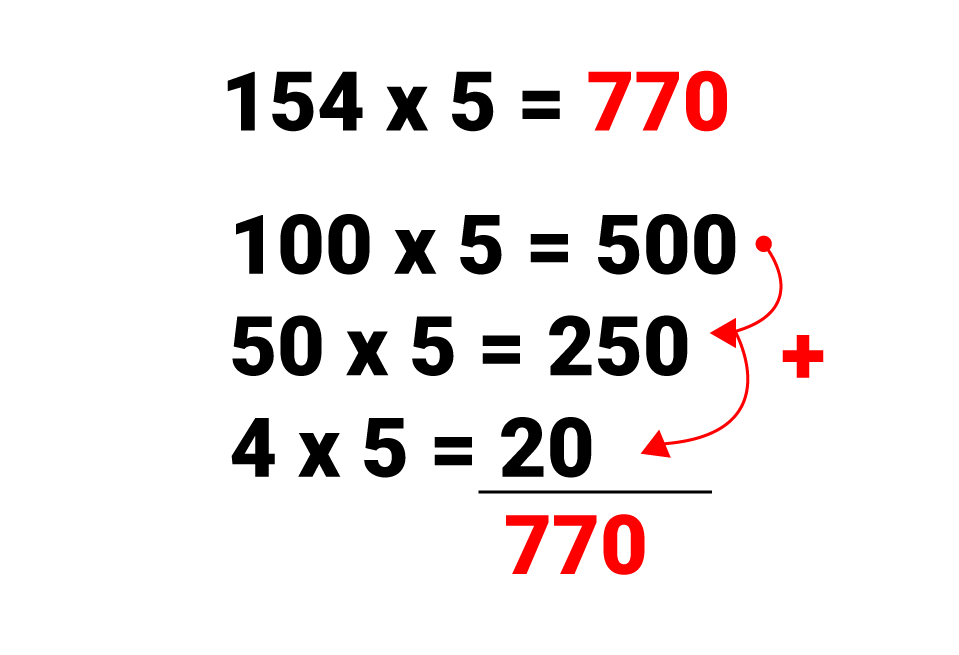
Proponha situações-problemas nas quais os estudantes possam escolher suas estratégias de resolução e, em seguida, discutam sobre elas:
Para os alunos:
1) O capitão Nestor está orgulhoso de seu novo navio de 2 andares e 240 cabines para acomodar os passageiros. 110 cabines são no 1º andar. Quantas cabines ficam no 2º andar?
2) A vendedora Rosângela conseguiu vender 5 bolsas no valor de R$ 15,00 cada uma e 3 sapatos no valor de R$ 90,00 cada um. Quanto ela recebeu por esses itens?
3) Vamos fazer um jogo? Escolha um colega e forme uma dupla. Desafie seu colega a descobrir seu pensamento a partir da seguinte sentença: “Pensei em um número, adicionei outro número e obtive o seguinte resultado.”
Você poderá revelar apenas dois números nessa sentença. Vamos ver quem consegue calcular? Caso seja necessário, pense em uma dica para ajudar seu colega de dupla.
Veja o exemplo:
“Pensei em número, adicionei 15 e obtive 40. Em que número pensei?”
Dica: O número que eu pensei tem 2 dezenas.
CRIAÇÃO/AVALIAÇÃO
Para os alunos:
Um jogo que pode ser colocado como uma estratégia de registro para a avaliação do desenvolvimento da habilidade de cálculo mental é o jogo “Cálculo Mental” – Adição e Subtração ou a versão Multiplicação, disponíveis em https://www.noas.com.br/ensino-fundamental-1/matematica/calculo-mental-adicao-e-subtracao/ e https://www.noas.com.br/ensino-fundamental-1/matematica/calculo-mental-multiplicacao/.
O primeiro passo do jogo é clicar no botão iniciar (botão amarelo na parte inferior). Em seguida, aparecerá uma operação e algumas opções. O jogador deverá identificar a resposta correta e clicar no resultado. Cada jogada tem um tempo determinado para ser respondida. Em caso de acerto, aparecerá uma mensagem informando que está correto e passará para a próxima operação. Em caso de erro, aparecerá a resposta correta antes de ir para a próxima jogada. Ao final de 20 jogadas é mostrado o desempenho, com a quantidade de erros e acertos.

