ÁREA DE CONHECIMENTO: MATEMÁTICA
COMPETÊNCIA (BNCC):
- Geral:
Competência 5 – Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
- Específicas:
Competência 2 – Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
Competência 3 – Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
Competência 5 – Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
HABILIDADE (BNCC):
(EF04MA19) – Reconhecer simetria de reflexão em figuras e em pares de figuras geométricas planas e utilizá-la na construção de figuras congruentes, com o uso de malhas quadriculadas e de softwares de geometria.
OBJETIVO
Apresentar ferramentas digitais de matemática para trabalhar o eixo estruturante Pensamento Computacional – Reconhecimento de Padrões e o conceito de simetria.
SEQUÊNCIA DIDÁTICA
Esta proposta apresenta duas possibilidades de ferramentas tecnológicas digitais para trabalhar a unidade temática Geometria proposta pela BNCC, considerando o estudo das simetrias com a manipulação de representações de figuras geométricas planas em quadriculados e com o recurso de softwares.
Um importante conceito a ser discutido ao se trabalhar com geometria é o reconhecimento de padrões, ou seja, as similaridades, as características que se repetem em algumas situações-problemas que, quando reconhecidas, podem ser exploradas e discutidas para serem solucionadas.

© Freepik
ORIENTAÇÕES PARA O PROFESSOR:
PONTO DE PARTIDA
Relembre com os estudantes o conceito de simetria: aquilo que pode ser dividido em partes, sendo que ambas as partes devem coincidir perfeitamente quando sobrepostas. Comente que o eixo que define a divisão é uma linha (eixo de simetria), real ou imaginária, que atravessa o centro da figura. Neste momento, proponha a construção de figuras em folhas de papel quadriculadas, solicitando que os desenhos sejam entregues aos colegas para reproduzirem as figuras originais.
PROBLEMATIZAÇÃO
Para trabalhar mais sobre simetria de reflexão apresente aos estudantes o jogo Mosaico Espelho que apresenta uma figura iniciada para que seja finalizada seguindo o padrão apresentado. Neste jogo, uma malha quadriculada é apresentada com uma figura dividida por um eixo vertical e o outro lado em branco. Para jogar é necessário clicar nas cores dispostas do lado direito e clicar na malha quadriculada seguindo o padrão apresentado, depois, clicar em Verificar. Se algum espaço estiver errado, será retirado da figura, mas se todos estiverem corretos, o jogo marcará um ponto e, clicando na seta do lado direito, passará para a próxima figura.
INTERVENÇÃO
Espera-se que os estudantes possam identificar que o jogo permite um reconhecimento, por meio da contagem dos quadrados e uma regularidade a partir da metade da figura apresentada.
Esse é um bom momento para ouvir as formas de resolução utilizadas pelos estudantes e discutir sobre outras possibilidades de resolução apresentando a discussão sobre pontos simétricos.
Dando continuidade ao trabalho, apresente a possibilidade de praticar a simetria de reflexão ao completar a grafia de algumas letras do alfabeto, por exemplo, na letra A, temos um eixo de simetria vertical, na letra B temos um eixo de simetria horizontal e na letra H temos os eixos vertical e horizontal.

Em relação aos pontos simétricos comente que a letra A tem um eixo vertical de simetria, e que os pontos podem ser marcados como referência para sua reflexão. Assim, temos o ponto que inicia o segmento, o ponto médio, em que marcamos o “corte” da letra A e o ponto que indica o fim do segmento.
Se seguirmos esses três pontos é só traçar outros segmentos do lado oposto, como na figura abaixo:
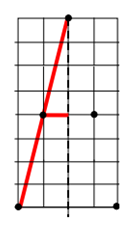
Para trabalhar os pontos simétricos podemos utilizar a ferramenta do Geogebra para criar imagens simétricas em relação a uma reta.
Acesse ao site e clique com o botão direito para aparecer a opção Malha:
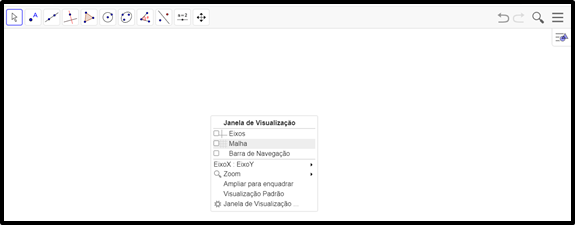
Selecione a ferramenta Segmento:

Deslize o mouse para marcar a metade da grafia da letra A:

Selecione a opção Reta:

Deslize o mouse para marcar o eixo vertical:

Selecione a opção Reflexão em Relação a uma Reta:

Selecione os pontos marcados e clique sobre a reta – eixo vertical:

Este será o resultado:

Comente com os estudantes sobre os pontos simétricos definidos anteriormente e se foram reproduzidos de forma simétrica.
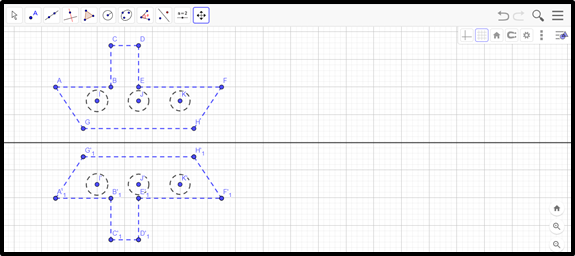
Desafie os estudantes a produzirem outras figuras de forma simétrica, utilizando o software:
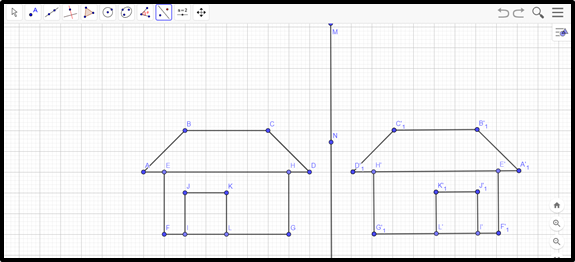
CRIAÇÃO/AVALIAÇÃO
Como avaliação, observe se os estudantes reconhecem as características e padrões que uma figura simétrica precisa apresentar e o que é um eixo de simetria.
COMPARTILHAMENTO
Para compartilhar a atividade, solicite que os estudantes façam uma exposição das construções de imagens simétricas produzidas no Geogebra. Vocês podem fazer uma exposição virtual, salvando as imagens e preparando uma apresentação digital ou expondo as imagens impressas.
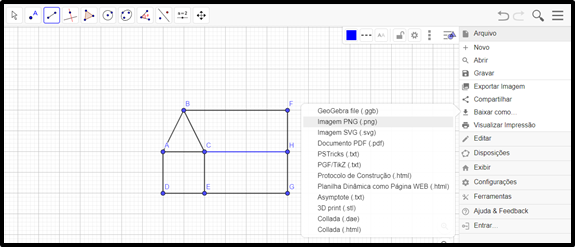
Dica: Baixe o arquivo no formato de imagem. Ao lado da lupa clique nas três linhas, vá em baixar arquivo e imagem PNG.
Atividade para os estudantes disponível em: <https://www.digipuzzle.net/minigames/mozaics/mozaics_mirror.htm?language=portuguese&linkback=../../pt/jogoseducativos/infantil/index.htm>.
Para os alunos:
Olá, vamos para mais um jogo?
O Mosaico Espelho apresenta uma figura iniciada e você precisará finalizá-la seguindo o padrão apresentado.
Perceba que a figura está dividida ao meio, por uma reta, você sabe por quê? Essa linha reta será o nosso eixo de simetria, ou seja, tomaremos por base essa linha para reconhecer o padrão da metade da figura e, então, completar o espaço em branco como se a imagem estivesse refletida em um espelho.
Para jogar, clique nas cores dispostas do lado direito, depois, clique na malha quadriculada seguindo o padrão apresentado. Quando terminar, clique em Verificar. Se algum espaço estiver errado, será retirado da figura, mas se todos estiverem corretos, o jogo marcará um ponto. Clicando na seta do lado direito, você poderá passar para a próxima figura.
Disponível em: <https://www.geogebra.org/classic#geometry>.
Você já ouviu falar sobre o Geogebra?
Ele é um site criado para utilizar a tecnologia no ensino e na aprendizagem da Matemática. Possui várias funções super interessantes e uma versão para celular que pode até mesmo apresentar as suas criações em realidade virtual!
Para começarmos a conhecer esse site vamos explorar um pouquinho sobre as possibilidades de criar imagens em 2D. Siga essas dicas e solte a imaginação para produzir as suas próprias figuras de forma simétrica:
Acesse o site, clique com o botão direito para aparecer a opção Malha:
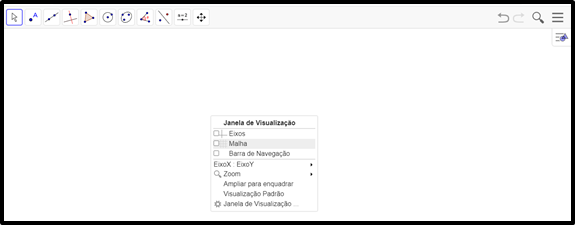
Selecione a ferramenta Segmento:

Deslize o mouse e vá marcando os pontos para construir a sua figura. Você também poderá inserir círculos em sua figura, para isso, selecione a ferramenta Círculo: Centro & Raio:
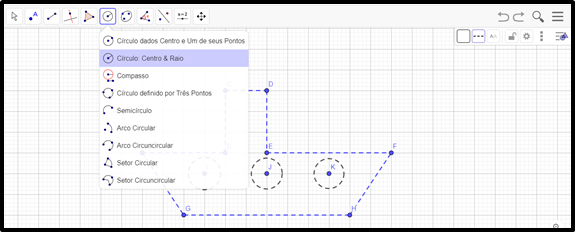
Selecione a opção Reta:

Deslize o mouse para marcar o eixo vertical ou horizontal:
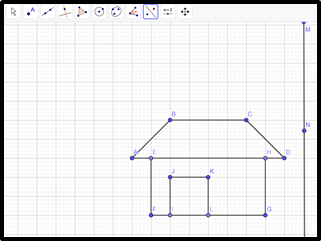
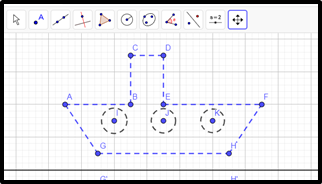
Selecione a opção Reflexão em Relação a uma Reta:

Selecione a imagem, clique na reta e este será o resultado: